The Class 9 is an important year in a student’s life and Maharashtra State Board Maths 1 is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 9 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete Maharashtra State Board Class 9 Maths 1 Book syllabus.
Practice set 4.1 Page no: 61
1. From the following pairs of numbers, find the reduced form of ratio of first number to second number.
i. 72, 60
ii. 38, 57
iii. 52, 78
Solution:
(i) Given 72,60
Reduced form of ratio of first number to second number:
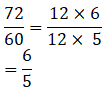
(ii) Given 38, 57
Reduced form of ratio of first number to second number:
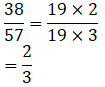
(iii) Given 52, 78
Reduced form of ratio of first number to second number:
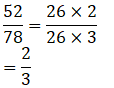
2. Find the reduced form of the ratio of the first quantity to second quantity.
i. 700 Rs, 308Rs.
ii. 14Rs, 12 Rs.40 paise.
iii. 5 litre, 2500 ml
iv. 3 years 4 months, 5 years 8 months
v. 3.8 kg, 1900 gm
vi. 7 minutes 20 seconds, 5minutes 6 seconds.
(iv) Given 3 years 4 months, 5 years 8 months
3 years = 3 × 12 = 36 months
∴ 3 years 4 months = 40 months
5 years = 5 × 12 = 60
∴ 5 years 8 months = 68 months
∴ Reduced form of the ratio of 40 months and 68 months is:
(v) Given 3.8 kg, 1900 gm
3.8 kg = 3.8 × 1000 = 3800 gm
∴ Reduced form of the ratio of 3800 gm and 1900 gm is:
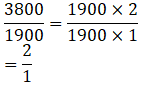
(vi) Given 7 minutes 20 seconds, 5minutes 6 seconds.
7 minutes = 7 × 60 = 420 seconds
∴ 7 minutes 20 seconds = 440 seconds
5minutes = 5 × 60 = 300 seconds
∴ 5 minutes 6 seconds = 306 seconds
∴ Reduced form of the ratio of 440 seconds and 306 seconds is:
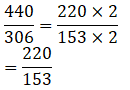
3. Express the following percentages as ratios in the reduced form.
(i) 75: 100
(ii) 44: 100
(iii) 6.25%
(iv) 52: 100
(v) 0.64%
Solution:
(i) Given 75: 100
Reduced form of the ratio of 75:100 is:
(ii) Given 44:100
Reduced form of the ratio of 44:100 is:
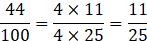
(iii) Given 6.25%
Reduced form of 6.25% is:
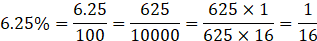
(iv) Given 52:100
Reduced form of the ratio of 52:100 is:
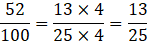
(v) Given 0.64%
Reduced form of 0.64% is:
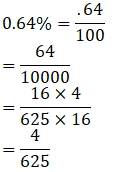
4. Three persons can build a small house in 8 days. To build the same house in 6 days, how many persons are required?
Solution:
Let the persons required to build a house in 6 days be x.
Days required to build a house and number of persons are in inverse proportion.
∴ 6 × x = 8 × 3
∴ 6 x = 24
∴ x = 4
∴ 4 persons are required to build the house in 6 days.
5. Convert the following ratios into percentage.
(i) 15: 25
(ii) 47: 50
(iii) 7/10
(iv) 546/600
(v) 7/16
Solution:
(i) Given 15: 25
= 15/25
= ((15/25) × 100) %
= (15 × 4) %
= 60 %
(ii) Given 47: 50
= 47/50
= ((47/50) × 100) %
= (47 × 2) %
= 94 %
(iii) Given 7/10
= ((7/10) × 100) %
= (7 × 10) %
= 70 %
(iv) Given 546/600
= ((546/600) × 100) %
= (546/6) %
= 91 %
(v) Given 7/16
= ((7/16) × 100) %
= (7 × 6.25) %
= 43.75 %
6. The ratio of ages of Abha and her mother is 2: 5. At the time of Abha ’s birth her mother’s age was 27 year. Find the present ages of Abha and her mother.
Solution:
Given the ratio of ages of Abha and her mother is 2 : 5.
Let the common multiple be x.
∴ Present age of Abha = 2x years and
Present age of Abha’s mother = 5x years
According to the given condition, the age of Abha’s mother at the time of Abha’s birth = 27 years
∴ 5x – 2x = 27
∴ 3x = 27
∴ x = 9
∴ Present age of Abha = 2x = 2 x 9 = 18 years
∴ Present age of Abha’s mother = 5x =5 x 9 = 45 years
The present ages of Abha and her mother are 18 years and 45 years respectively.
7. Present ages of Vatsala and Sara are 14 years and 10 years respectively. After how many years the ratio of their ages will become 5: 4?
Solution:
Given present age of Vatsala = 14 years
Present age of Sara = 10 years
Let after x years, the ratio of their ages will be 5:4.
∴ Age of Vatsala after x years = (14 + x) years
Age of Sara after x years = (10 + x) years
Ratio of their ages = 5:4
On cross multiplying, we get:
56 + 4x = 50 + 5x
⇒ 5x – 4x = 56 – 50
⇒ x = 6
∴ After 6 years, their ages will be 20 years and 16 years and ratio of their ages will be 5:4.
8. The ratio of present ages of Rehana and her mother is 2: 7. After 2 years, the ratio of their ages will be 1: 3. What is Rehana ’s present age?
Solution:
The ratio of present ages of Rehana and her mother is 2 : 7
Let the common multiple be x.
∴ Present age of Rehana = 2x years and Present age of Rehana’s mother = 7x years
After 2 years,
Rehana’s age = (2x + 2) years
Age of Rehana’s mother = (7x + 2) years
According to the given condition,
After 2 years, the ratio of their ages will be 1 : 3
∴ 2x+27x+2 = 13
∴ 3(2x + 2) = 1(7x + 2)
∴ 6x + 6 = 7x + 2
∴ 6 – 2 = 7x – 6x
∴ 4 = x
∴ x = 4
∴ Rehana’s present age = 2x = 2 x 4 = 8 years
∴ Rehana’s present age is 8 years.
Practice set 4.2 Page no: 63
1. Using the property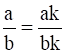 
, fill in the blanks substituting proper numbers in the following.
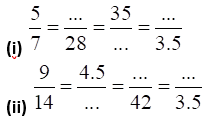
Solution:
(i) Let
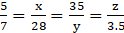
∴ on comparing first two equalities, we get:
5/7 = x/28
Cross multiply and get:
7x = 28 × 5
⇒ x = 4 × 5 = 20
Now, compare the first and third equalities and get:
5/7 = 35/y
Cross multiply and get:
5y = 7 × 35
⇒ y = 7 × 7 = 49
Now, compare the first and fourth equalities and get:
5/7 = z/3.5
Cross multiply and get:
7z = 5 × 3.5
⇒ 7z = 5 × (35/10)
⇒ z = 5 × (5/10)
⇒ z = 25/10 = 2.5
∴
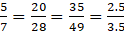
(ii) Let
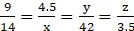
∴ On comparing first two equalities, we get:
9/14 = 4.5/x
Cross multiply and get:
9x = 14 × 4.5
⇒ x = 14 × 0.5 = 7
Now, compare the first and third equalities and get:
9/14 = y/42
Cross multiply and get:
14y = 9 × 42
⇒ y = 9 × 3 = 27
Now, compare the first and fourth equalities and get:
9/14 = z/3.5
Cross multiply and get:
14z = 9 × 3.5
⇒ z = 9 × (3.5/14)
⇒ z = 9 × (0.25)
⇒ z = 2.25
∴
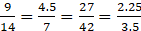
2. Find the following ratios.
(i) The ratio of radius to circumference of the circle.
(ii) The ratio of circumference of circle with radius r to its area.
(iii) The ratio of diagonal of a square to its side, if the length of side is 7 cm.
(iv) The lengths of sides of a rectangle are 5 cm and 3.5 cm. Find the ratio of its perimeter to area.
Solution:
(i) Let r be the radius of a circle.
Circumference of circle = 2πr
Ratio of radius to circumference of circle = r/2πr
= 1/2π
= 1: 2π
(ii) Let r be the radius of a circle.
Circumference of circle = 2πr
Area of the circle =2πr2
Ratio of radius to circumference of circle = 2πr/πr2
= 2/r
= 2: r
(iii) Side of square = 7 cm
Diagonal of square = √2 × side = 7√2 cm
Ratio of diagonal of a square to its side = 7/7√2
= 1/√2
= 1: √2
(iv) Length of rectangle = 5 cm
Breadth of rectangle = 3.5 cm
Perimeter of rectangle = 2(Length + Breadth)
= 2(5+3.5)
= 2(8.5)
= 17 cm
Area of rectangle = Length × Breadth
= 5 × 3.5
= 16.5 cm2
Ratio of Perimeter to area of rectangle
= 17/16.5
= 170/165
= 34/33
3. Compare the following pairs of ratios.
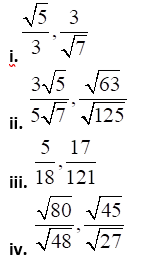
v.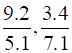 
Solution:
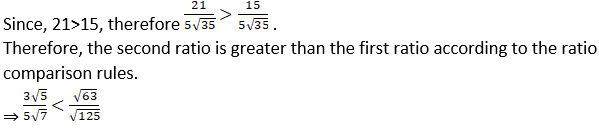
Therefore, both the ratios are equal, according to the ratio comparison rules.
⇒
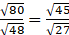
Practice set 4.3 Page no: 70
1. If a/b = 7/3 then find the values of the following ratios.
Solution:
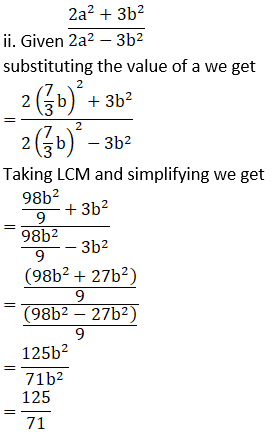
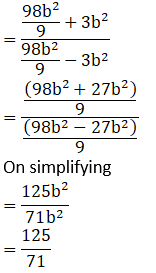
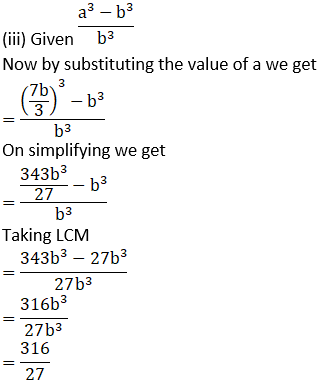
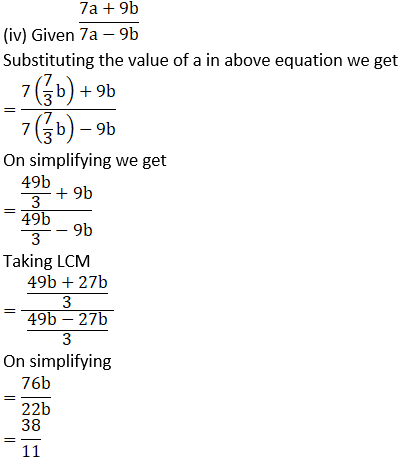
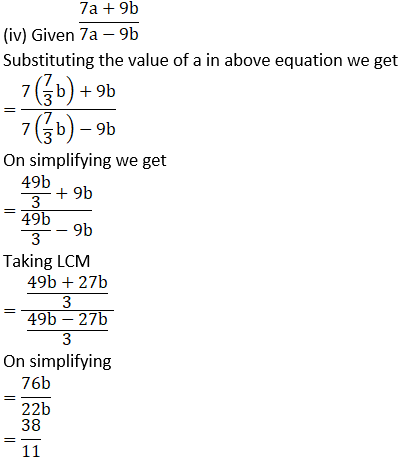
2. If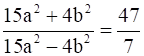 
then find the values of the following ratios.
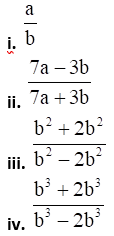
Solution:
(i) Given:
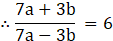
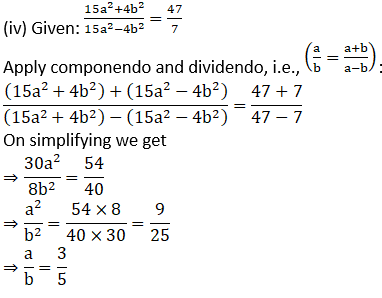
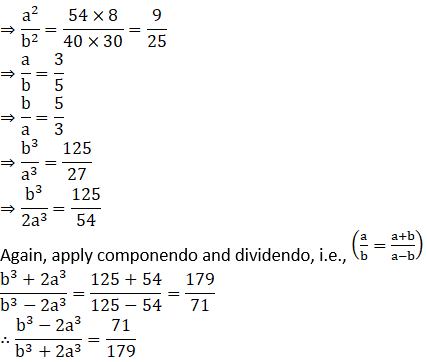
Practice set 4.4 Page no: 73
1. Fill in the blanks of the following
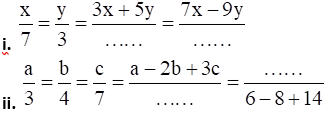
Solution:
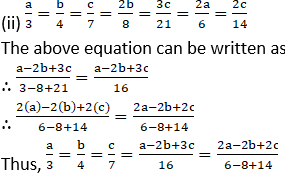
2. 5m-n=3m+4n, then find the values of the following expressions.
Solution:
(i) Given: 5m – n = 3m + 4m
⇒ 5m – 3m = 4n + n
On simplifying we get
⇒ 2m = 5n
On rearranging
⇒ m/n = 5/2
⇒ m2 /n2 = 25/4
Apply componendo and dividendo:
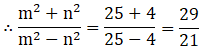
= 29:21
(ii) Given: 5m – n = 3m + 4m
⇒ 5m – 3m = 4n + n
On simplifying we get
⇒ 2m = 5n
On rearranging
⇒ m/n = 5/2
⇒ 3m/4n = 15/8
Apply componendo and dividendo:
= 23: 7
Practice set 4.5 Page no: 77
1. Which number should be subtracted from 12, 16 and 21 so that resultant numbers are in continued proportion?
Solution:
Let x be the number that should be subtracted from 12, 16, 21 so that the numbers remain in continued proportion.
Numbers a, b and c are said to be continued proportion if b2 = ac.
∴ From the definition of continued proportion, we get:
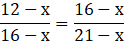
⇒ (16 –x)2 = (12 –x) (21 –x)
On expanding the above equation, we get
⇒ 256 + x2 – 32x = 252 –33x + x2
⇒-32x + 33x = 252 – 256
⇒ x= -4
∴ -4 should be subtracted from 12, 16, 21 so that the numbers remain in continued proportion.
2. If (28 –x) is the mean proportional of (23 –x) and (19 –x) then find the value of x.
Solution:
A number b is said to be mean proportional of two numbers a and c if b2 = ac.
∴ From the definition of mean proportion, we get:
(28 –x)2 = (23 –x) (19 –x)
On expanding the above equation, we get
⇒ 784 + x2 – 56x = 437 –42x + x2
⇒-56x + 42x = 437 – 784
⇒ -14x= -347
⇒ x = 347/14
3. Three numbers are in continued proportion, whose mean proportional is 12 and the sum of the remaining two numbers is 26, then find these numbers.
Solution:
Let the numbers be x, y, z.
As the numbers are in continued proportion, therefore
y2 = xz ……………… (1)
Also, the mean proportion = 12
∴ y = √xz = 12
⇒ xz = 144 …………… (2)
It is given that the sum of remaining two numbers = 26
∴ x + z = 26
⇒ x = 26 – z
Put the value of x in equation (2):
(26 – z) z = 144
Expanding and simplifying we get
⇒ 26z – z2 = 144
⇒ z2 – 26z + 144 = 0
⇒ z2 – 8z – 18z + 144 = 0
⇒ z (z –8) – 18 (z – 8) = 0
⇒ (z –8) (z –18) = 0
⇒ z = 8 or z = 18
∴ x = 26 – 8 or x = 26 – 18
⇒ x = 18 or x = 8
y = 12
∴ The numbers in proportion be 8, 12, 18 or 18, 12, 8.
4. If (a + b+ c) (a –b + c) = a2 + b2 + c2 , show that a, b, c are in continued proportion.
Solution:
Given: (a + b+ c) (a –b + c) = a2 + b2 + c2
On multiplying we get
⇒ a2 –ab + ac + ab –b2 + bc + ca – bc + c2 = a2 + b2 + c2
⇒ a2 –ab + ac + ab –b2 + bc + ca – bc + c2 –a2 –c2 = b2 + b2
⇒ 2ac = 2b2
⇒ b2 = ac
∴ a, b, c are in continued proportion.
5. If a/b = b/c and a, b, c >0, then show that,
i. (a + b+ c) (b – c) = ab – c2
ii. (a2
+ b2
) (b2
+ c2
) = (ab + bc)2
iii. (a2
+ b2
)/ab = (a + c)/b
Solution:
(i) Given: a/b = b/c
⇒ b2 = ac
Consider (a + b+ c) (b – c) = ab – ac + b2 – bc + cb – c2
= ab – ac + ac – c2 (∵ b2 = ac)
= ab – c2
(ii) Given a/b = b/c
⇒ b2 = ac
Consider (a2 + b2 ) (b2 + c2 ) = a2 b2 + a2 c2 + b2 b2 + b2 c2
= a2 b2 + ac(ac)+ b2 (ac)+ b2 c2 (∵ b2 = ac)
= a2 b2 + b2 (ac)+ b2 (ac)+ b2 c2 (∵ b2 = ac)
= a2 b2 + 2b2 (ac)+ b2 c2
= a2 b2 + 2ab2 c+ b2 c2
= (ab + bc)2
(iii) Given: a/b = b/c
⇒ b2 = ac
Consider (a2 + b2 )/ab = (a2 + ac)/ab (∵ b2 = ac)
= (a + c)/b
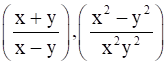
6. Find mean proportional of
Solution:
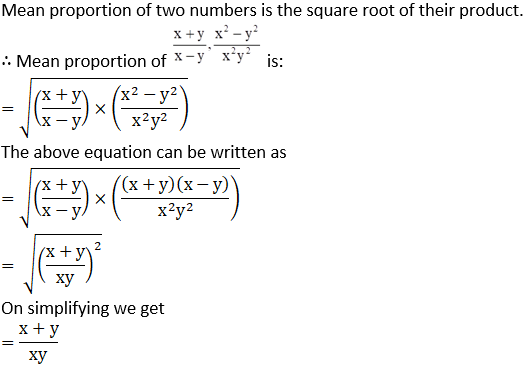
On simplifying we get
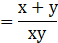
Problem set 4 Page no: 77
1. Select the appropriate alternative answer for the following questions.
i. If 6: 5 = y: 20 then what will be the value of y?
A. 15
B. 24
C. 18
D. 22.5
Solution:
B. 24
Explanation:
Given 6:5 = y:20
⇒ 6/5 = y/20
Cross multiply and get:
5y = 6 × 20
⇒ y = 6 × 4 = 24
∴ Option B is correct.
ii. What is the ratio of 1 mm to 1 cm?
A. 1: 100
B. 10: 1
C. 1: 10
D. 100: 1
Solution:
A. 1: 100
Explanation:
We know that 1 cm = 100 mm
∴ 1mm: 1cm
⇒ 1mm: 100mm
= 1: 100
∴ Option A is correct.
iii. The ages of Jatin, Nitin and Mohasin are 16, 24 and 36 years respectively. What is the ratio of Nitin’s age to Mohasin’s age?
A. 3: 2
B. 2: 3
C. 4: 3
D. 3: 4
Solution:
B. 2: 3
Explanation:
Given Nitin’s age = 24 years
Mohasin’s age = 36 years
∴ Ration of Nitin’s age to Mohasin’s age = 24:36
= 24/36
= 2/3
= 2:3
∴ Option B is correct.
iv. 24 Bananas were distributed between Shubham and Anil in the ratio 3 : 5, then how many bananas did Shubham get?
A. 8
B. 15
C. 12
D. 9
Solution:
D. 9
Explanation:
Total bananas = 24
Ratio in which the bananas are divided = 3:5
Let number of bananas Shubham got = 3x
∴ Number of bananas Anil got = 5x
∴ 3x+5x = 24
⇒ 8x = 24
⇒ x = 3
∴ Shubham got (3 × 3) = 9 bananas.
Thus, option D is correct.
v. What is the mean proportional of 4 and 25?
A. 6
B. 8
C. 10
D. 12
Solution:
C. 10
Explanation:
Mean proportional of two numbers a and b = √(ab)
∴ Mean proportional of 4 and 25 = √ (4 × 25)
= √100 = 10
2. For the following numbers write the ratio of first number to second number in the reduced form.
i. 21, 48
ii. 36, 90
iii. 65, 117
iv. 138, 161
v. 114, 133
Solution:
(i) Ratio of 21 and 48 in the reduced form:
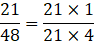
(To simplify, break the numbers in simpler form)
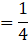
∴ Ratio of 21 and 48 in reduced form is 1:4.
(ii) Ratio of 36 and 90 in the reduced form:
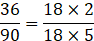
(To simplify, break the numbers in simpler form)
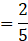
∴ Ratio of 36 and 90 in reduced form is 2:5.
(iii) Ratio of 65 and 117 in the reduced form:
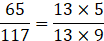
(To simplify, break the numbers in simpler form)
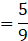
∴ Ratio of 65 and 117 in reduced form is 5:9.
(iv) Ratio of 138 and 161 in the reduced form:
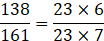
(To simplify, break the numbers in simpler form)
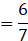
∴ Ratio of 138 and 161 in reduced form is 6:7.
(v) Ratio of 114 and 133 in the reduced form:
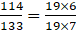(To simplify, break the numbers in simpler form)
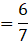
∴ Ratio of 114 and 133 in reduced form is 6:7.
3. Write the following ratios in the reduced form.
i. Radius to the diameter of a circle.
ii. The ratio of diagonal to the length of a rectangle, having length 4 cm and breadth 3 cm.
iii. The ratio of perimeter to area of a square, having side 4 cm.
Solution:
(i) Let r be the radius of the circle.
Let d be the diameter of the circle.
Diameter = 2 × Radius
∴ Ratio of radius to diameter in the reduced form = Radius: Diameter
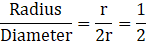
∴ Ratio of radius to diameter in the reduced form = 1:2
(ii) Given: Length of rectangle = l = 4 cm
Breadth of rectangle = b = 3 cm
Diagonal of rectangle = √ (l2 + b2 )
= √ (16 + 9)
= √25 = 5
∴ Diagonal of rectangle = 5 cm
Ratio of diagonal to the length of a rectangle = 4:5
(iii) Given: Side of square = 4 cm
Perimeter of square = 4 × Side = 4 × 4 = 16 cm2
Area of the square = (Side)2 = (4)2 = 14 cm2
The ratio of perimeter to area of a square = 16:14 = 8:7
4. Check whether the following numbers are in continued proportion.
i. 2, 4, 8
ii. 1, 2, 3
iii. 9, 12, 16
iv. 3, 5, 8
Solution:
(i) Three numbers ‘a’, ‘b’ and ‘c’ are said to be continued proportion if a, b and c are in proportion, i.e. a: b∷ b:c
or b2 = ac
Here, a = 2, b = 4 and c = 8
∴ (4)2 = 2 × 8
⇒ 16 = 16, which holds true.
∴ 2, 4, 8 are in continued proportion.
(ii) Three numbers ‘a’, ‘b’ and ‘c’ are said to be continued proportion if a, b and c are in proportion, i.e. a: b∷ b:c
or b2 = ac
Here, a = 1, b = 2 and c = 3
∴ (2)2 = 1 × 3
⇒ 4 = 3, which does not hold true.
∴ 1, 2, 3 are not in continued proportion.
(iii) Three numbers ‘a’, ‘b’ and ‘c’ are said to be continued proportion if a, b and c are in proportion, i.e. a: b∷ b: c
or b2 = ac
Here, a = 9, b = 12 and c = 16
∴ (12)2 = 9 × 16
⇒ 144 = 144, which holds true.
∴ 9, 12, 16 are in continued proportion.
(iv) Three numbers ‘a’, ‘b’ and ‘c’ are said to be continued proportion if a, b and c are in proportion,
i.e. a: b∷ b: c
or b2 = ac
Here, a = 3, b = 5 and c = 8
∴ (5)2 = 3 × 8
⇒ 25 = 24, which does not hold true.
∴ 3, 5, 8 are not in continued proportion.
5. a, b, c are in continued proportion. If a = 3 and c = 27 then find b.
Solution:
Given: a, b, c are in continued proportion.
Three numbers ‘a’, ‘b’ and ‘c’ are said to be continued proportion if a, b and c are in proportion, i.e. a: b∷ b:c
or b2 = ac
Here, a = 3, c = 27
∴ (b)2 = 3 × 27
⇒ b2 = 81
⇒ b = ±√81 = ±9
∴ b = -9 or 9
6. Convert the following ratios into percentages.
i. 37: 500
ii. 5/8
iii. 22/30
iv. 5/16
v. 144/1200
Solution:
(i) Given 37: 500 = 37/500
= ((37/500) × 100) %
= (37/5) %
= 7.4 %
(ii) Given 5/8 = ((5/8) × 100) %
= (5 × 12.5) %
= 62.5 %
(iii) Given 22/30 = ((22/30) × 100) %
= (220/3) %
= 73.33 %
(iv) Given 144/1200 = ((144/1200) × 100) %
= (144/12) %
= 12 %